Why do Cars Move? - Entropy Explained
We explore one of the most fundamental laws of nature, which can not only explain why cars move, but why virtually any macroscopic process evolves in a given direction.

I know, there are wheels, a motor, pistons and all that sophisticated engineering, but that is not what this article is about. This article is about the most fundamental reason why cars move, or really, why any macroscopic system evolves in a predictable direction.
So, why do cars move?
To answer this question, I have constructed a simple simulation model of a car. As a disclaimer up front, I should say that this model does not cover every aspect of a car. Quite the contrary, it omits a lot of quite important aspects. I hope you are open to let go of these things for the moment, and I promise that this will uncover an unobstructed view on this very basic principle that makes cars (and a lot of other things) move. Along the way, we will get intuitive access to entropy, a quantity which is unfortunately often poorly understood, because it is frequently wrongly equated with disorder.
The simplest simulation model of a car
Here are some observations about cars that I think should be reflected even in the simplest model of a car. (I am talking about one of these old school versions that are still burning fuel.)
A car is some sort of container...
...with wheels.
There is a tank with fuel in it.
There is some sort of motor linked to the wheels.
This motor connects the fuel tank with the environment and rotates as fuel atoms travel through it.
The following video shows the model I came up with.

The simplest simulation model of a car
There are a lot of simplifications in the model, so please take it with a grain of salt!
Fuel atoms are depicted as orange marbles, and in the beginning of the simulation all fuel atoms start in the fuel tank. Atoms are quite complicated fellows on their own, but I chose a very simple approach to model their behavior. I assumed that they move around randomly. For gases, this is actually not such a bad approximation.
In each simulation step, one random marble and one random direction (up, down, left, right) are chosen. If there is nothing blocking the way, the chosen marble is moved one step in the chosen direction. If the way is blocked by another marble or a wall, nothing happens, and the simulation continues with the next step, where again a random marble is selected and potentially moved. Such randomly evolving simulations, by the way, are called Monte Carlo simulations.
There are two somewhat special fields in the simulation. An atom moving left in the bottom left field of the fuel tank will move through the motor into the environment and will push the car forward. An atom moving right in the bottom right field of the grid representing the environment, will move through the motor into the fuel tank and push the car backward.
Now, where do you expect to find the car after the simulation has evolved for a while, when all marbles started in the fuel tank? Well, in the video above you have already seen an example, where the car ended up further to the right compared to where it started, but that is probably just a coincidence, right? After all, it is a random simulation. The car could end up anywhere!
Well, let's repeat the simulation a couple of times. The following video shows 4 simulations in parallel.

Parallel Simulation Runs
Like before, the car always ends up further to the right compared to where it started. It sometimes takes a step back, but in the long run it moves to the right in all cases. Why is that? Even though the marbles move around completely randomly, the car does not seem to behave so randomly after all.
This becomes clear, if we look at the number of possibilities to find the car in the different positions. If we treat the marbles as indistinguishable, there is only one possibility how the marbles can be arranged if the car is in the start position. All marbles are in the fuel tank, and all fields in the fuel tank are occupied.
For the car to be one step ahead, one marble needs to be outside the car. There are considerably more possibilities how the marbles can be arranged in this state. The single marble in the environment could be in any of the 25 environment fields. There is also a vacancy in the fuel tank which could be at any of the 9 fuel tank fields. Together, these are 25*9=225 possibilities for the car to be in this position.
For the next few positions, with fewer marbles in the tank, the number of possibilities how the marbles can be arranged becomes even larger. The following video shows the number of possibilities for each location of the car, and a systematic sweep through at least some possibilities for each car location.
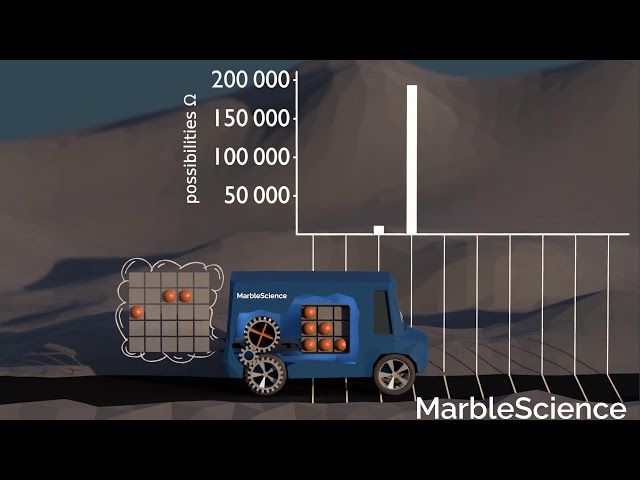
Number of Possibilities
As we can see, there are vastly more possibilities for the car to be in one of the positions further ahead. After the simulation has run sufficiently long, it is, for example, more than 15 mio. times more likely to find the car 7 steps ahead compared to finding it in the start position. So, why does the car move forward? It is simply by far the likeliest thing to happen!
Cars move because it is likely, and it is likely because there are so many more possibilities for the atoms from the fuel to be distributed somewhere in the environment compared to being confined in a small fuel tank. Distributing all the atoms while the motor is turning forward is a very likely process to happen, and in contrast, it is a very unlikely process for all these distributed, randomly moving atoms to find their way back into the motor to push it back.
Maybe you ask yourself now: "Okay, but I have never seen a car move back and forth randomly. Unless it is broken, it always moves like it is supposed to. There is nothing random about it." That's a fair point, and I will address it in a moment, but I would like to introduce entropy first.
Entropy
In the previous video we have seen that the number of possibilities for the different car locations varies across multiple orders of magnitude. Working with numbers ranging across multiple orders of magnitude is sometimes inconvenient. In the plot of the possibilities, for example, the number of possibilities of the first few locations is no longer visible once the scale changes to millions. A common trick to circumvent such problems with numbers of different orders of magnitude is to work with the logarithm of a quantity instead.
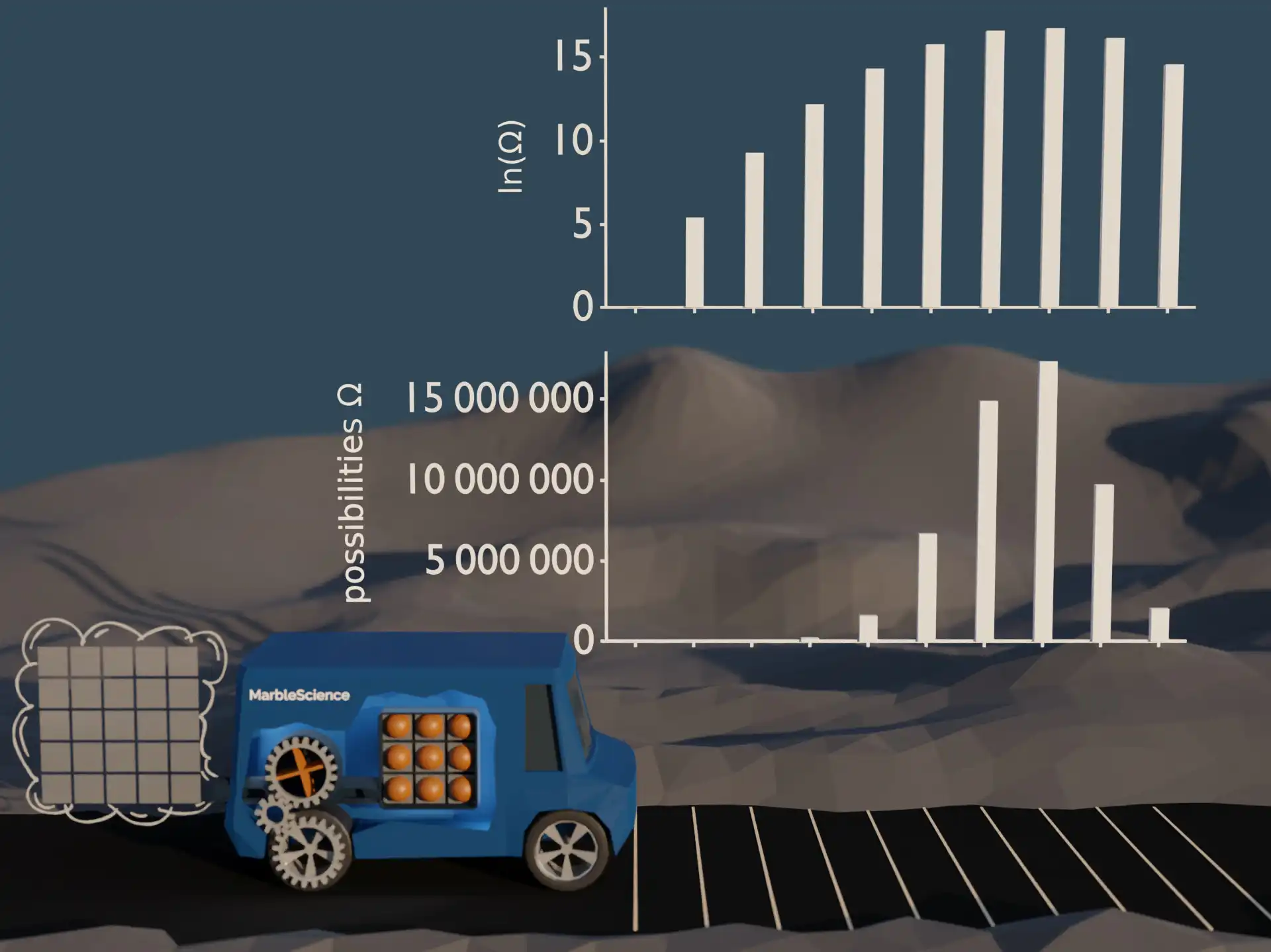
Logarithm of the number of possibilities
This quantity, ln(Ω), the natural logarithm of the number of equal probable possibilities, is called entropy. S = ln(Ω) it is as simple as that!
Sometimes you also come across this definition of Entropy: S = kBln(Ω). Don't worry about this multiplication with the Boltzmann constant kB too much. Multiplying with a constant simply changes the unit of some quantity. For example, if you multiply a length in centimeters with the appropriate constant, then you get the same length in inches. It's the same in the case of entropy.
Irrespective of the unit, entropy is simply a measure of the number of possibilities how something could be realized. In this context, the terms "macrostate" and "microstate" are often used. In the car simulation, for example, we could consider each possible location of the car to be a macrostate. From a macroscopic perspective, this is what we see — a car in different locations. If we take a look on a more detailed level, however, we can see that each of these macroscopic states consists of one or multiple microstates. In the car simulation example, these are all the different arrangements of marbles that are possible for a given location of the car. The entropy of a macrostate tells you how many microstates (possibilities) it involves.
The second law of thermodynamics
As a measure of the number of possibilities, entropy is closely related to probability. Under the premise that all possibilities are equally likely, it is more likely for a system to evolve into a state with high entropy compared to a state with low entropy, simply because a high entropy tells us that there are a lot of possibilities to observe the system in that state. The car moving forward from the start position is an example for that.
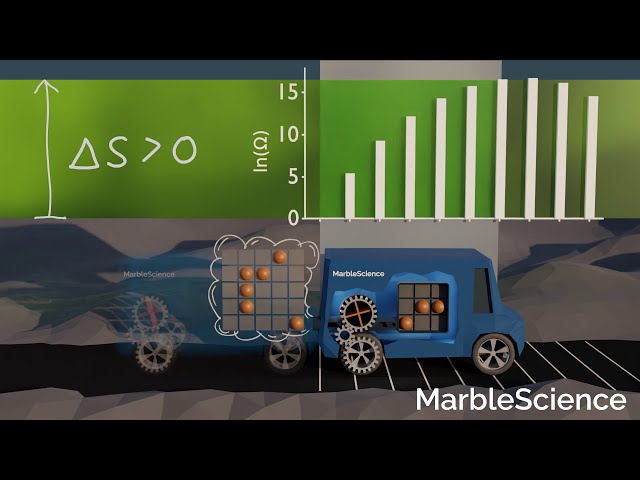
Car Moving Forwards
The process of the car moving forward from the start position has a positive ΔS. In other words, the end state of the process has a larger entropy compared to the initial state. In yet other words, there are more possibilities for the end state to occur compared to the initial state. Consequently, we wouldn't be surprised if this process occurred.
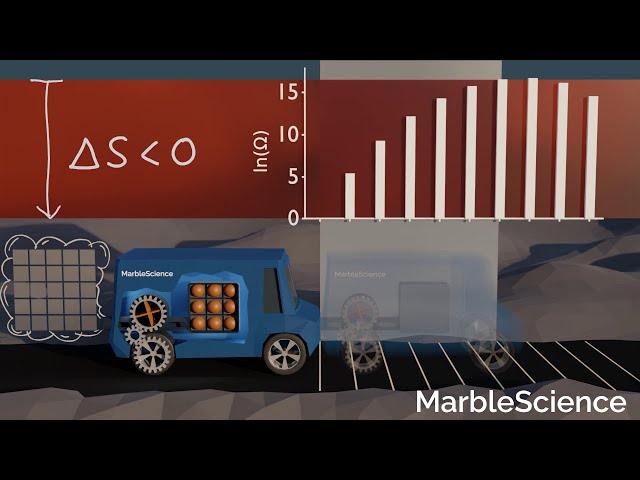
Car moving backwards
In the opposite case, if the car moves back to the starting position, ΔS is negative. In other words, the end state of the process has a lower entropy compared to the initial state. In yet other words, there are fewer possibilities for the end state to occur compared to the initial state. Consequently, we would be quite surprised if this process occurred.
Based on the above findings, processes with a positive ΔS are processes that tend to happen regularly, and processes with a negative ΔS are processes that rarely happen. This is a very important finding because it allows us to evaluate if some process might happen or not. So important in fact that it found its place as the second fundamental law of thermodynamics.
There are many other ways how the second law has been formulated. This ranges from humorous statements like: "You can't shovel manure into the rear end of a horse and expect to get hay out its mouth." (William M. White) to more general formulations like: "the total entropy of an isolated system can never decrease over time". The later formulation is also often expressed with the simple formula: ΔS ≥ 0.
You might have noticed that the later formulation of the second law contradicts what we have seen before. A negative ΔS only means that a process is unlikely to happen. So, why would someone make a bold statement like: "the total entropy of an isolated system can never decrease over time"? This leads us back to a point I had already raised earlier: "I have never seen a car move back and forth randomly. Unless it is broken, it always moves like it is supposed to. There is nothing random about it." So which is it? Are changes with a negative ΔS merely unlikely or are they somehow impossible?
The law of large numbers
In the car simulation model with 9 marbles, the probability of finding the car in the start position compared to finding it in the most likely position is about 1 in 17 million. That's roughly comparable to winning the lottery — very unlikely, but it still happens sometimes. The following figure shows again the number of possibilities for each location of the car.
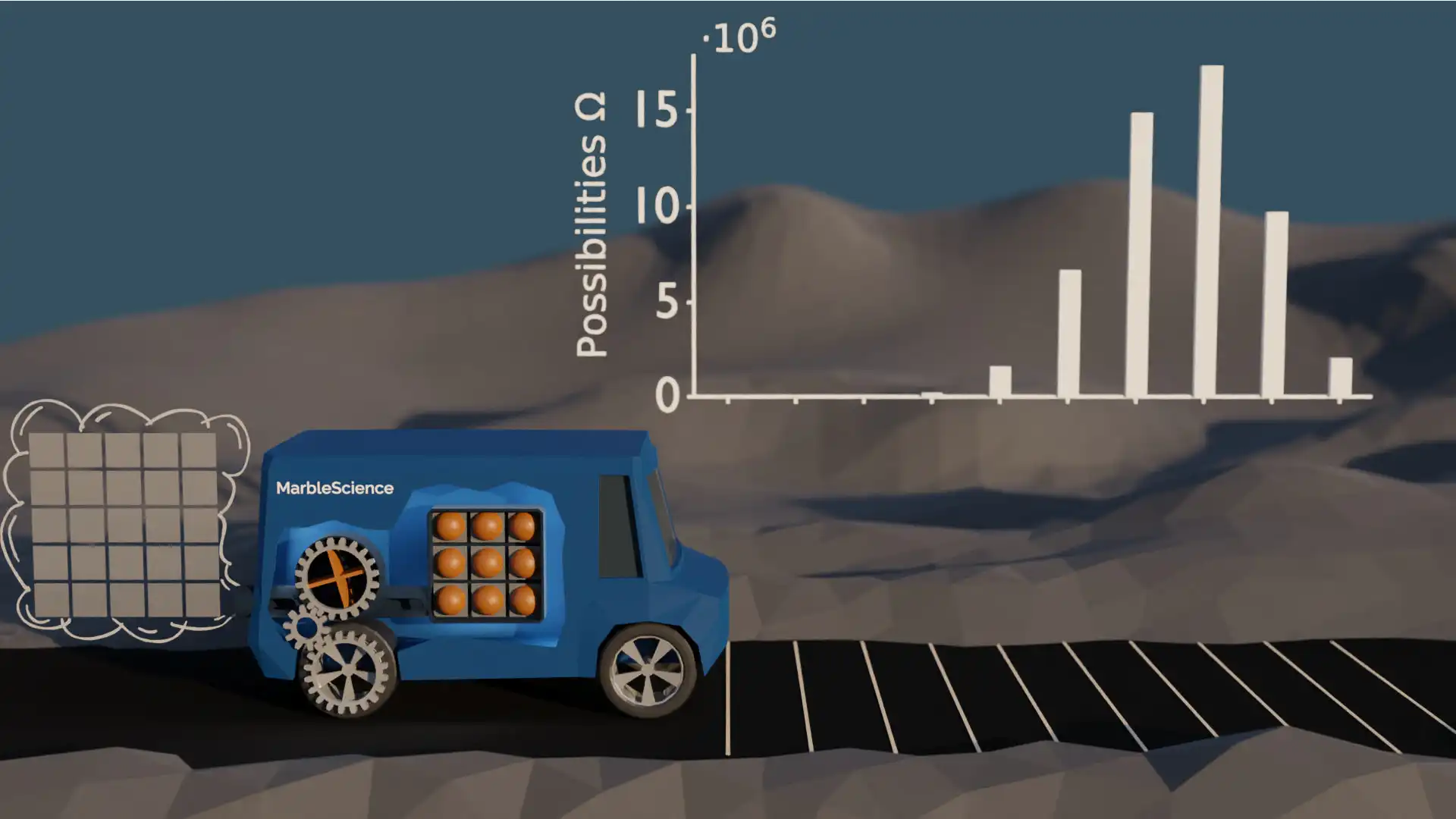
Possibilities with 9 Marbles
Obviously, a real car has not just 9 giant atoms in its fuel tank. So let's make the model more realistic by changing the number and size of the marbles. The following figure shows the number of possibilities for a car with 36 fuel marbles. As the number of marbles increased by a factor of 4, I also decreased the step size of the car to a fourth accordingly.
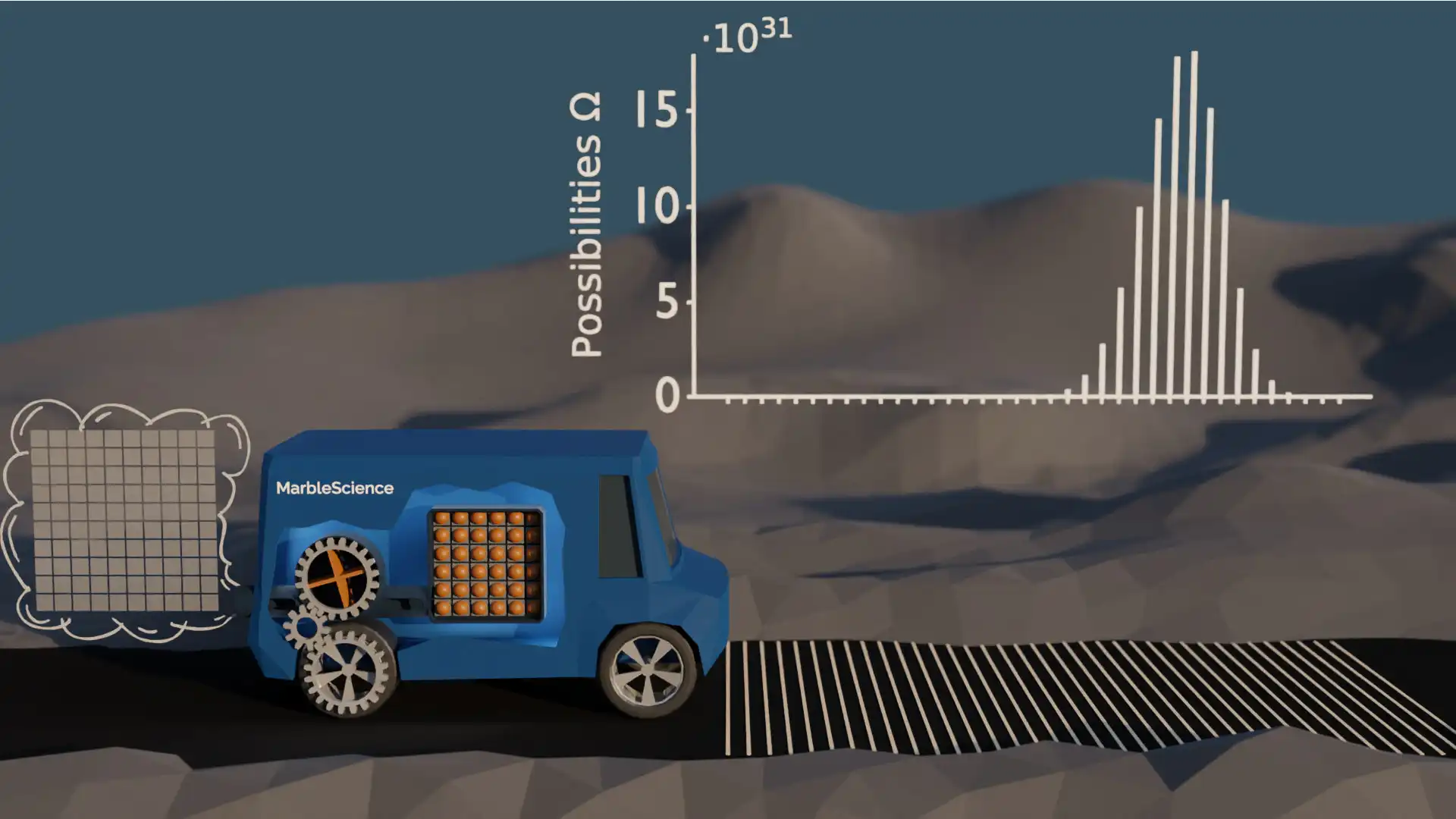
Possibilities with 36 Marbles
Let's again increase the number of marbles by a factor of 4 and see what happens.
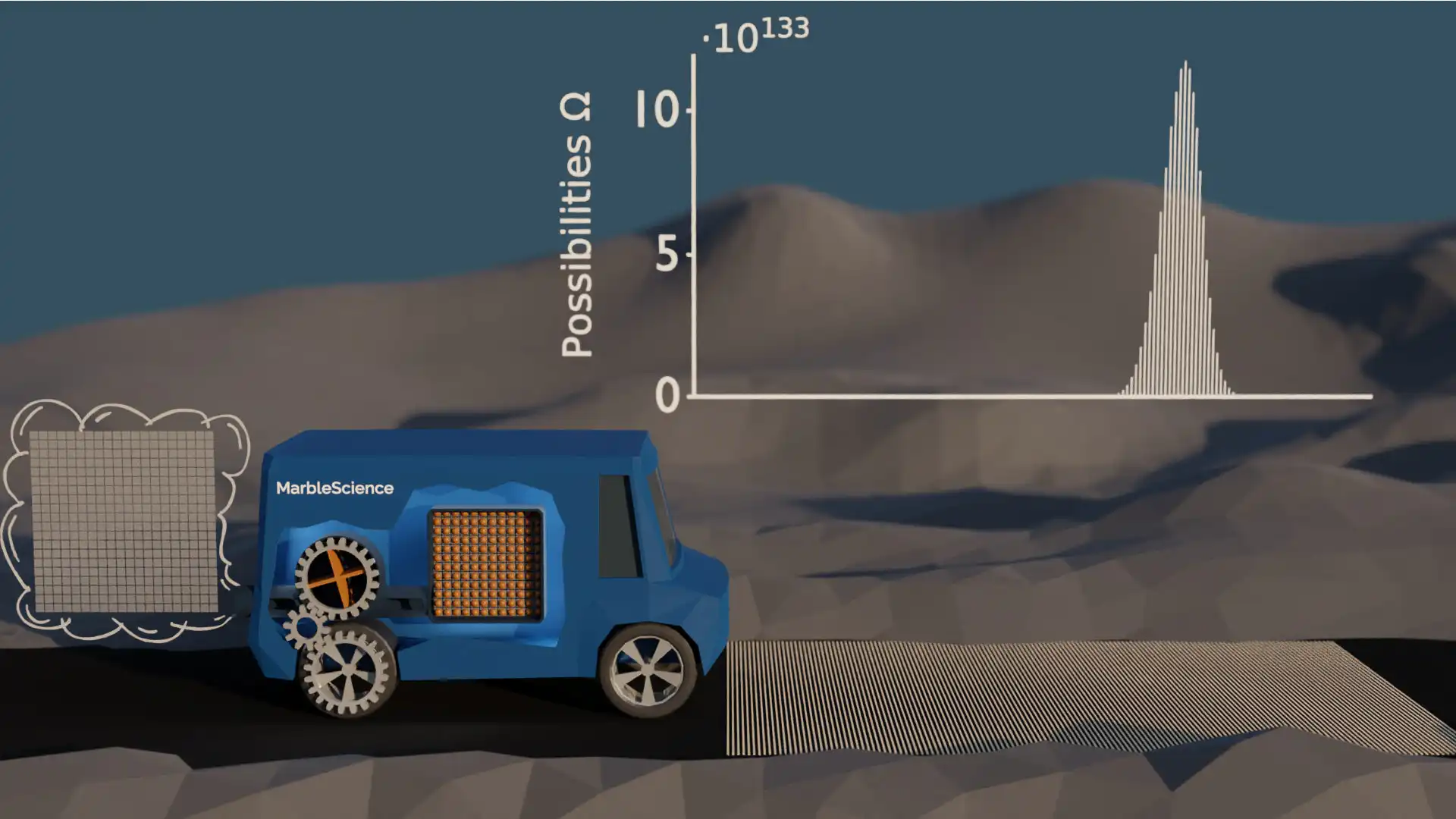
Possibilities with 144 Marbles
There are two things that we can observe here. With each increase of the number of marbles, the possibility distribution becomes more narrow, and the height of the maximum is increased. In the last case, there is still just one possibility for the car to be in the start position, but there are more than 10134 possibilities for the car to be in the most likely position.
It is hard to grasp how large this number (10134) actually is, but let me try to give you some idea. The number of atoms on our planet is something like 1050. Including our planet, our solar system, our galaxy, and everything else we can see, the observable universe is estimated to contain roughly 1080 atoms. That is still nowhere near the number of possibilities for the car to be in the most likely position! We should also keep in mind that this is the result for a model with 144 marbles. This number is still ridiculously small compared to the number of atoms which are involved in each stroke of a real engine. With larger numbers, the possibility distribution would be even more narrow and the most likely car position would be even more dominant.
So is it possible for the entropy in an isolated system to go down? Is it possible for all the atoms to randomly find their way back through the exhaust pipe, through the motor, back into the fuel tank? Technically yes, but the concept that we just explored, which is called "the law of large numbers", shows us that for a system with a large number of randomly behaving entities, the probability for something like this to happen can quickly become insanely small. For a system with a lot of randomly behaving entities, the possibility distribution becomes so narrow, and the most likely state becomes so dominant; the most likely outcome is essentially all we need to care about! All states outside the narrow vicinity of the most likely state are so unbelievably unlikely that we can safely ignore them.
Conclusion
Why does a car move? A car is driven by probability! It moves because there are far more possibilities how it could happen compared to how it could not happen. Fundamentally, on a microscopic scale, it is a random process. However, on a macroscopic scale, the result is still very predictable. The fate of the car does not depend on the behavior of a single atom. It depends on the average behavior of gazillions of atoms, and for a large number of atoms, this average behavior is absolutely dominated by the most likely result. The probability that such a system could evolve towards a state far away from the most likely state is so unbelievably small, beyond any scales that humans could think on, that we can safely ignore it. Randomness and causality are not in contradiction to each other. They just live on different levels of resolution!
In the end, the second law of thermodynamics basically just tells us: Likely things tend to happen; Unlikely things don't. It is really kind of a no-brainer if you think about it. The more difficult part, however, is to see why some things are so likely to happen. I hope this article helps you to see some of those things. Maybe, when the wind blows in your face, you will see how it is the most likely thing when atoms or molecules on average move from a region with lots of atoms to a region with fewer atoms. Maybe, when you observe any working machine, you will see how it is running because it is the most likely outcome. Maybe you take a breath and appreciate how all these atoms finding their way into your lung was simply the likeliest thing to happen.
