Monte Carlo Simulations

What is a Monte Carlo simulation?

The name ”Monte Carlo” refers to the city in Monaco, known for its casinos and gambling. ”Monte Carlo” is basically used as a synonym for randomness, and Monte Carlo simulations are simulations evolving in a deliberately random way.

Maybe that's a bit counterintuitive at first. How can something meaningful come out of a randomly evolving simulation? Shouldn't it precisely follow some sophisticated rule to give accurate results? Instead, we deliberately incorporate randomness into the simulation!? We will see why this can be helpful in the following example.

Simple example of a Monte Carlo simulation

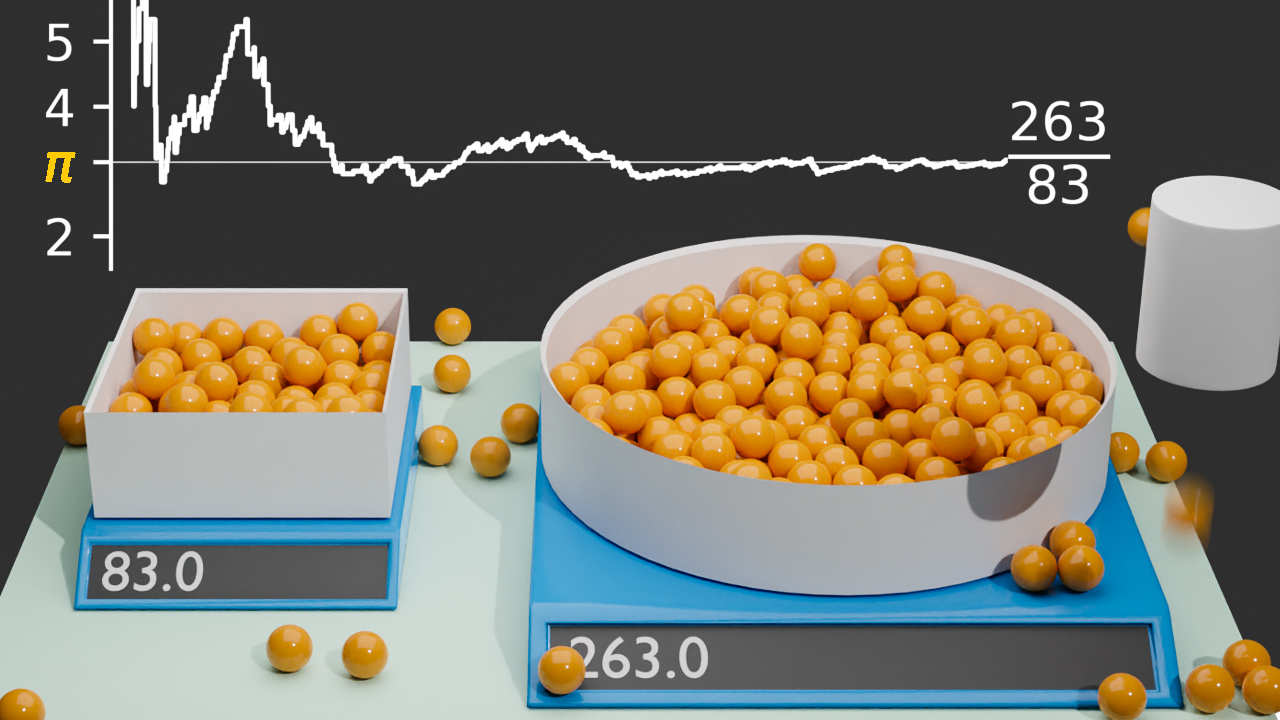
The following video contains a simple example of a Monte Carlo simulation. The (I don't know what to call it) "marble placer" moves around randomly above a rectangular table and drops marbles. On the table, there are two bowls. One with a square cross-section with an edge length of a, and one with a circular cross-section with a radius of a. Each of the bowls is placed on some sort of scale which allows us to measure how many marbles are in each bowl.

If we let this simulation evolve for a while and divide the number of marbles in the circular bowl by the number of marbles in the square bowl, the result happens to be roughly pi. Without any advanced math knowledge simply by randomly dropping marbles into two bowls we can estimate pi, a task which is not at all trivial.

When clicked, this video is loaded from youtube.com. See our privacy policy for details.

Determine pi with a Monte Carlo Simulation

So let's unpack what happened here. When we drop a marble in a uniformly random location, the probability for it to end up in one of the bowls is proportional to the bowl's cross-section area. When we repeat this random process over and over again, the number of marbles in a bowl will approach a value which is proportional to its cross-section area. The area of the square bowl in this example is a², and the area of the circular bowl is pi*a². That's how we get pi as the fraction of the two areas and consequently as the fraction of marbles in each bowl.

Ratio of Cross-sectional Areas

In the marble dropping example, we essentially determine an area by taking random samples. With each random sample we probe whether this specific location is inside or outside some area, and by taking enough samples we get a good idea of how big an area is.

Analogy outside the simulation world

The idea of obtaining random samples is probably quite familiar to you if you think about how real world studies outside of simulations are done. Let's say we wanted to make a study to determine the average body height of all people worldwide. In principle, we would need to know the height of each person worldwide and take the average of all these heights. Obviously, we can't go out and measure the height of billions of people. So what do we do?

We can measure the heights of a smaller group of people and hope that their average height is a good estimate of the average height of all people worldwide. There are two things that we need to consider to get a good estimate:

Firstly, the selection of the group needs to be unbiased. We can't just measure the height of the next 10 people we meet or the height of all our family members, as we might live in an area with especially tall or short people. Also, our family might not be a good representative for the world population. Instead, a good way to get an unbiased sample group would be to randomly select people worldwide.

Secondly, the group of measured people must not be too small. If we only measured the height of 5 people, we might have coincidentally picked 5 taller people. We can be more and more confident about the resulting average the more people we measure. In probability theory this is often referred to as the law of large numbers.

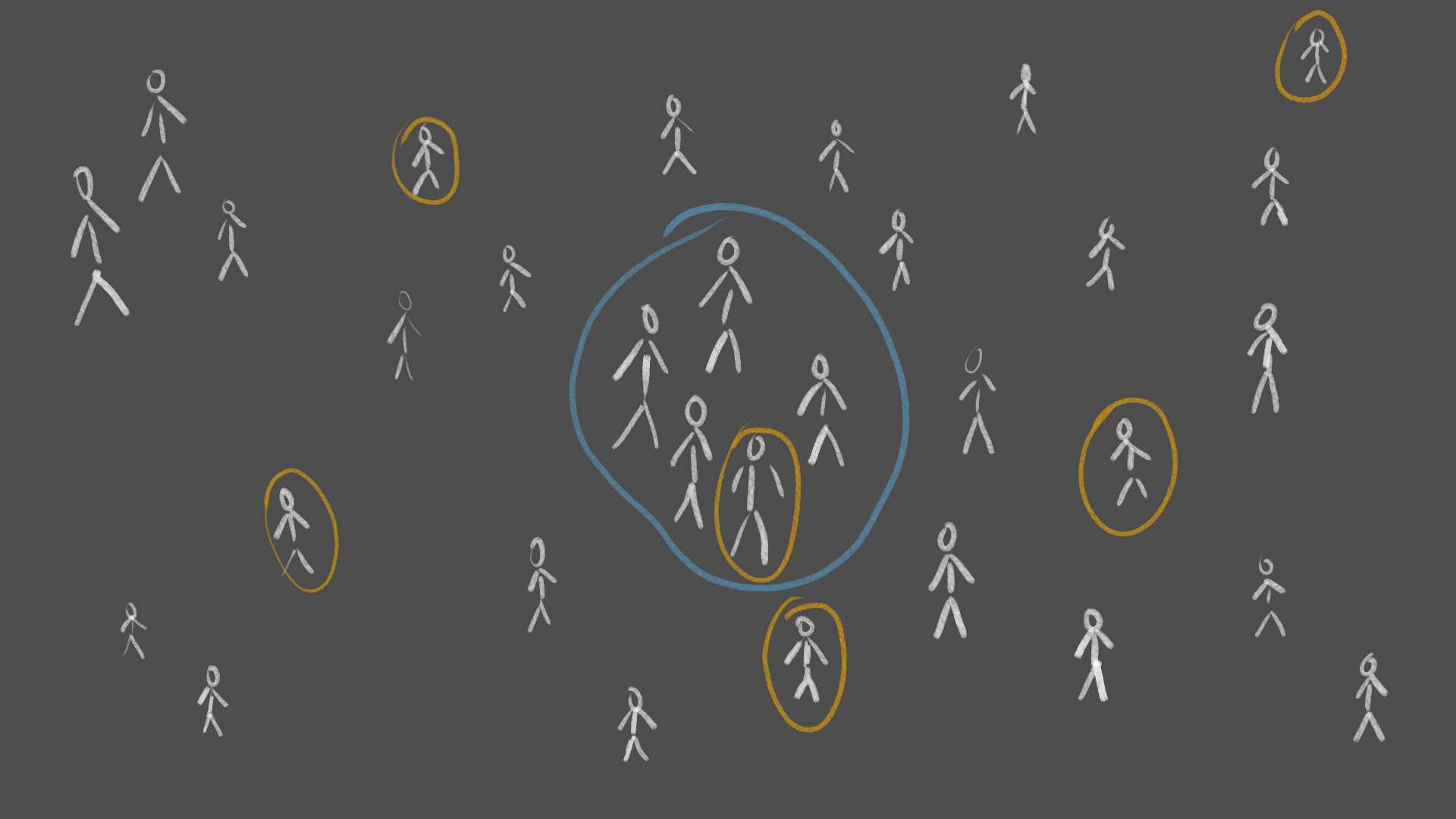
Systematic vs Random Selection

Back to simulations

The exact same is also true for Monte Carlo simulations. The core idea of a Monte Carlo simulation is that we can obtain a representative group of samples of some large population of possibilities if we allow the simulation to evolve randomly.

In the marble dropping example, in principle, we would need to test for every possible location whether the marble ends up inside or outside the bowl to determine its cross-section area precisely. Just like we, in principle, would need to measure the height of each person to determine the average height accurately. Instead, we can rely on randomly selected samples, and according to the law of large numbers, we can be more and more confident about the result the more samples we take.

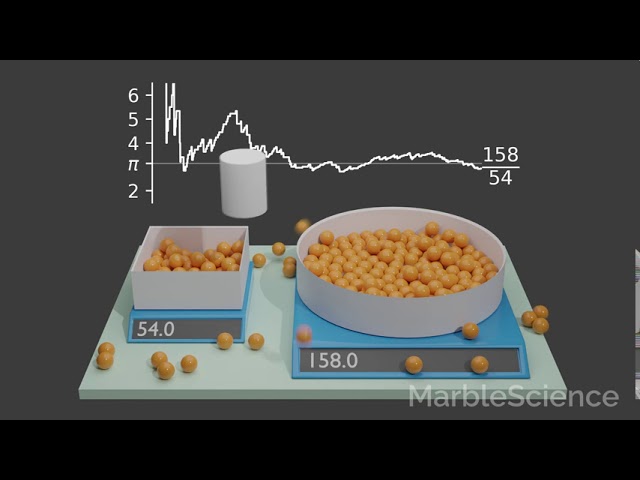
We can see this if we plot the fraction of marbles in both bowls over time. Initially the value is fluctuating heavily, but with more and more samples generated by the randomly evolving simulation, the fluctuations become smaller and smaller, and we can see that the value approaches the expected value of pi.

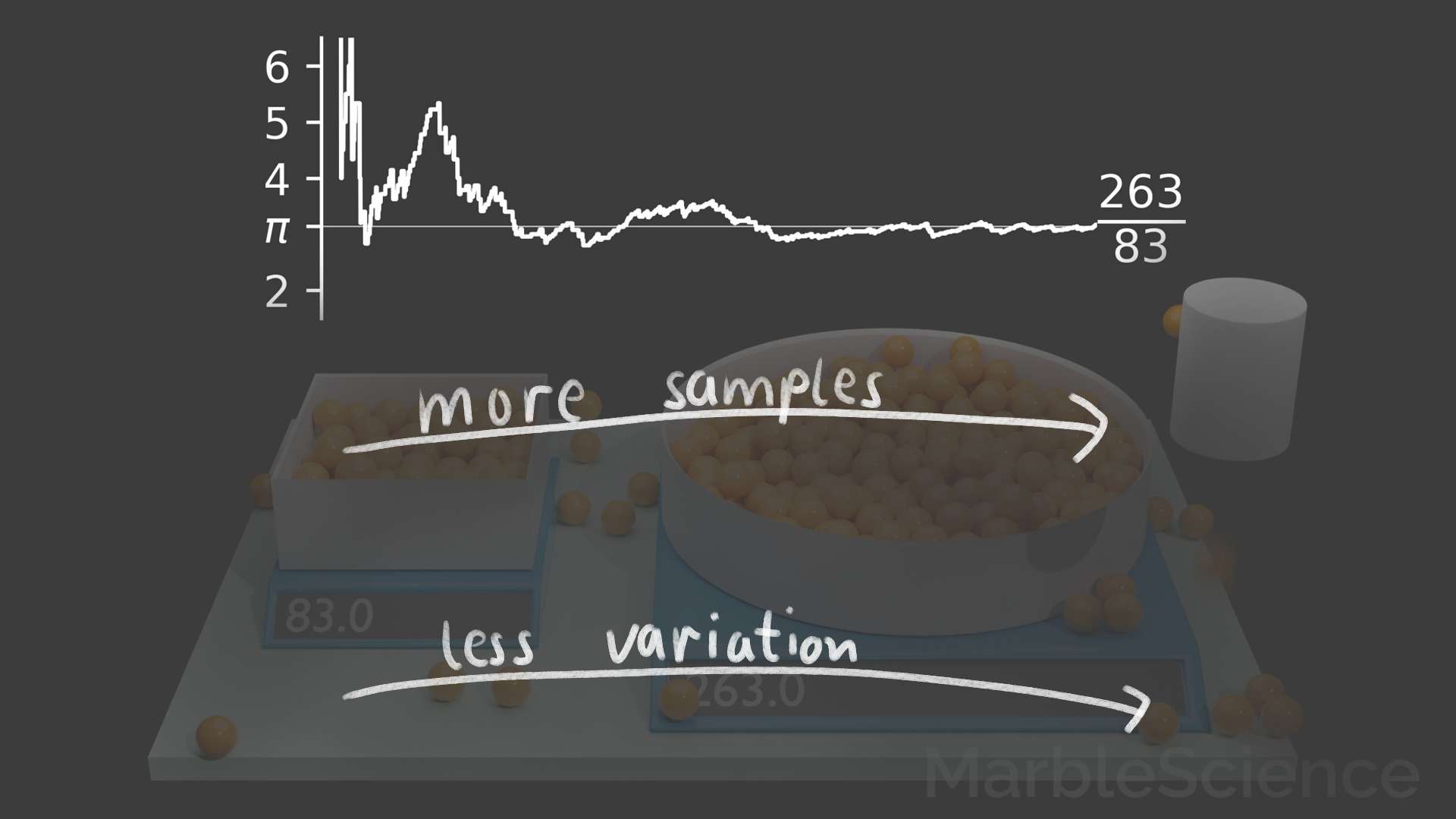
More Samples -> Less Variation

Monte Carlo Path Tracing

Using a Monte Carlo simulation to determine pi is an illustrative, but not really relevant example. However, the animation of randomly dropping marbles into bowls is actually a good example for a Monte Carlo simulation in yet another way.

Rendering such animations is all about simulating the flow of light. To get an accurate image, you need to find out how much light hits different areas of the scene. That is not an easy task if you consider that diffuse surfaces can scatter light in virtually any direction. Let's say we want to find out how much light hits the marked area in the simple example scene shown in the following figure.

Simple Illumination Example

In principle, we would need to evaluate all possible light paths to find out which fraction of them ends in the marked area to determine the illumination accurately.

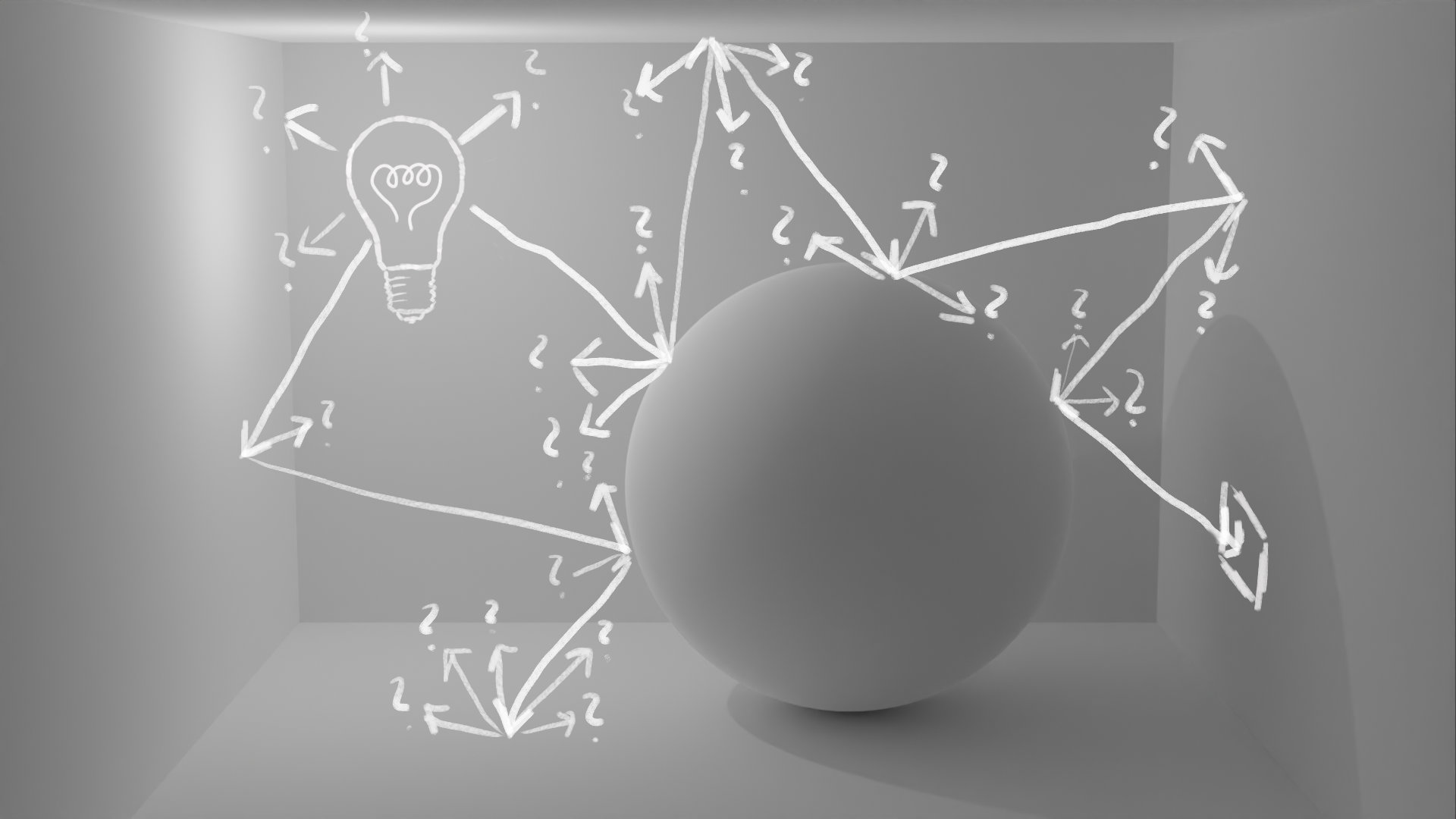
Attempt to Follow All Paths

So what can we do if we can't simulate all possible light paths? I hope, after reading the article up to this point, the answer is quite obvious. If we can't simulate all paths, the best we can do is to get a representative group of samples - and what is a good way to get an unbiased group of samples? We can employ randomness! Whenever we hit a diffuse surface, we simply randomly pick one of the infinitely many directions in which the light could be scattered.

One randomly simulated light path is not valuable on its own, but if we generate many sample paths, we can get a good idea of the illumination of the scene. We will see areas that are hit by many of the randomly generated light rays(brightly illuminated areas), and we will see other areas that are hit by few of the random light rays(darker areas).

Actually, if you think about it, counting the number of random light rays hitting some area is really not that different from counting the number of randomly dropped marbles hitting a bowl. In the marble dropping attempt to determine pi, we saw that we get less variation in the result, the more samples we take (the more marbles we drop). The same is also true for Monte Carlo path tracing as the following figure shows.

More Samples -> Less Variation

With more samples we get a less noisy result, but also the computational effort is increased. For large scenes or whole animations, this can become expensive very quickly. Many tricks have been developed to improve the performance of Monte Carlo path tracing. For example, it is common to reverse the light path. When the light paths are traced back from a camera, then naturally only paths ending in the camera are simulated. All the light paths that don't hit the camera are never simulated with this variant. Despite all the tricks, a production level path tracing algorithm might contain, it shares the simple idea of a randomly evolving simulation that all Monte Carlo simulations have in common.

Conclusion

Many problems involve an unfeasibly large number of possibilities. With Monte Carlo simulations, only a random subset of these possibilities are explored in a randomly evolving simulation. According to the law of large numbers, we can still get reasonable results if we gather enough of these random samples.