Why is it really cold in the mountains?

"Why is it cold on top of a mountain?" is one of these questions where most feel like they should know the answer, many seem to know the answer, but then somehow everyone tells a different story.

This is how, what I naively believed to be a quick Google search to brush up my knowledge, somehow turned into a month-long endeavor to come up with a good explanation.

This article is for you if you really want to know how it works. Buckle up for a deep dive! But don't worry, we will start very easy with a simple model of a stationary atmosphere, and we will add more complexity with gravity and convection (wind) later on.

Especially, wind blowing up a mountain and the associated expansion of air is often presented as the reason for cold mountains. This might not be entirely wrong, but we will see that it is at least a very twisted way to put it. Anyway, more about this later. Let's dive in!

Level 1 - What if the atmosphere was stationary?

To build a model of an atmosphere we first have to make some very basic considerations about heat and radiation.

• Objects that absorb radiation become warmer.
• Warm objects emit heat radiation.
• The intensity of the emitted radiation depends on the temperature.

Here is my attempt to incorporate these considerations in a simple model. I know it is not an atmosphere yet ;)

The glowing dots represent heat radiation. The color of the slab indicates its temperature. It turns more orangy (higher temperature) as it absorbs radiation. You should also be able to see that as it cools down fewer of the glowing dots are emitted, to reflect the weaker heat radiation at lower temperatures.

Let's build an Atmosphere

If we stack a bunch of these slabs, we get a simple model how heat is distributing in something with multiple layers.

We are pretty close to a model atmosphere already, but for a somewhat realistic model of our atmosphere we need a second kind of radiation. The sun mainly emits visible light, and we all know that the atmosphere is largely transparent for visible light. Otherwise, we couldn't see much.

Visible and infrared light

Visible light and long-wave heat (infrared) radiation are fundamentally the same electromagnetic radiation. They only differ in frequency. Very hot objects like the sun emit primarily high frequency radiation (visible light). Comparatively cold objects like the ground here on earth emit low-frequency radiation (infrared). See Planck's law for more information about that.

We can incorporate visible light in the model by introducing a second type of glowing dot. I chose white dots to represent visible light. To reflect the transparent nature of the atmosphere, I changed the program code for the white dots, such that they can only be absorbed by the lowest layer where the ground is.

Additionally, I changed the code such that heat is only emitted upwards or downwards. This makes it a bit less chaotic to look at, and it conveniently stops heat from leaking out to the sides.

Turn on the sun with the toggle at the bottom!

Over time, we can see that a beautiful temperature gradient is forming. The ground layer is heated up by the sun and starts to emit heat radiation. The intermediate layers absorb that heat radiation and start to emit themselves. They send heat radiation back and forth. The outermost layer is special because it can only receive heat radiation from below, but it still emits radiation to both sides. It directly loses heat into space. That is why it is always the coldest layer in the model.

But where are the mountains?

Now you might say: "Ok that explains why it is cold high above the ground, but it still doesn't explain why it is cold in the mountains." In the mountains, we might be high up, but we are still on the ground. Sunlight can be absorbed by the ground and directly heat up the air in the mountains.

We can simply add mountains to the model by raising the ground level in a part of the simulation:

If you keep the simulation running sufficiently long (use the fast-forward button), you can see that the layer above the mountains is still colder compared to the ground layer on the right. It absorbs the same radiation from the sun, but is still doesn't heat up as much.

A good way to think about cold mountain tops is to view the atmosphere as an insulation layer, just like the clothes you are wearing or the foamed material used to insulate houses. A thick insulating layer makes it difficult for heat to escape and leads to high temperatures below. A thin layer on the other hand can't suppress heat transfer as much and leads to lower temperatures. On top of mountain there is just not as much insulating atmosphere left above you.

With a thickness of the atmosphere of about 100 km (Kármán line), you might think that the height of a mountain doesn't play a big role. However, this is misleading because of the unequal distribution of air in the atmosphere. The atmosphere is much denser at the bottom. Actually, at an elevation of 5.6 km (in terms of air mass) already half of the atmosphere is below you.

Level 2 - But what about the thermosphere?

Now what if I told you that the outermost layer of our atmosphere (depends a bit on where you draw the boundary) is actually the warmest layer. Its name thermosphere comes from its high temperatures with more than 1000°C.

How can it be cold on top of a mountain if you are in between the warm sea level layer and the even hotter outer layers of the atmosphere?!

So far we have mainly ignored one important aspect of our atmosphere: its density gradient.

Gravity's effect on the atmosphere

Without gravity, gas tends to distribute equally in the available space, but if you activate the gravity in the simulation below, you can see that it becomes more crowded at the bottom. Gravity leads to a density gradient in the atmosphere. The air down in a valley is denser compared to the air high up the atmosphere.

We will come back to the thermosphere in a moment, but I want to make one other point while we are talking about gravity.

Some people claim that gravity alone should lead to lower temperatures in high altitude. They argue that atoms high up have more potential energy, and should therefore have less kinetic energy left. The speed (and with that the kinetic energy) of the atoms is correlated to the temperature of a gas. Therefore, more potential energy and less kinetic energy would result in a lower temperature.

We can simply test if that is the case by monitoring the average speed in the upper and lower half of the simulation:

As you can see if you activate gravity, the average speed again fluctuates around the same value for both halves. This is a generally important finding. Thermodynamic systems do not equilibrate to the same total energy, but to the same temperature.

In this case it means that gravity alone can not explain any temperature differences.

Back to the thermosphere

Let's incorporate the density gradient caused by gravity into our model atmosphere. I use the opacity of a layer to indicate its density. The density of a layer has three important effects:

In a low density layer...

• the probability for heat radiation to be absorbed is lower.
  (there are just fewer atoms/ molecules that could be hit by any radiation)
• heat radiation is emitted less frequently for the same given temperature.
  (there are just fewer atoms/ molecules that could emit anything)
• the same amount of radiation absorbed leads to a larger change in temperature.
  (the same amount of energy is distributed among fewer atoms)

Additionally to the density gradient, I also introduced a third type of glowing dot - violet dots to represent the radiation absorbed in the outer part of the atmosphere.

Now there is a lot going on in the simulation, and the temperature of the outer layers tends to fluctuate quite a bit because auf the small size of the simulation and their low density. Anyway, you should be able to see that we can indeed get colder layers below a hot outer layer.

I you watch closely, you can see that heat radiation emitted in the middle layers now has quite a good chance to make it directly into space. Due to its low density, the outer layer is largely transparent for heat radiation. Also, due to its low density, it emits little heat despite its high temperature.

The outer layer is there, and it is hot, but with its low density, it just doesn't play such a big role for the layers below.

The temperature profile of earth's atmosphere

In our real atmosphere, there is actually a second layer that is heated up by absorbing some of the sun's radiation. I'm sure you know this layer, but you might have never thought about the effect it has on the atmosphere's temperature. It is the ozone layer which absorbs a large part of the ultraviolet light. This leads to the following temperature profile of our atmosphere:

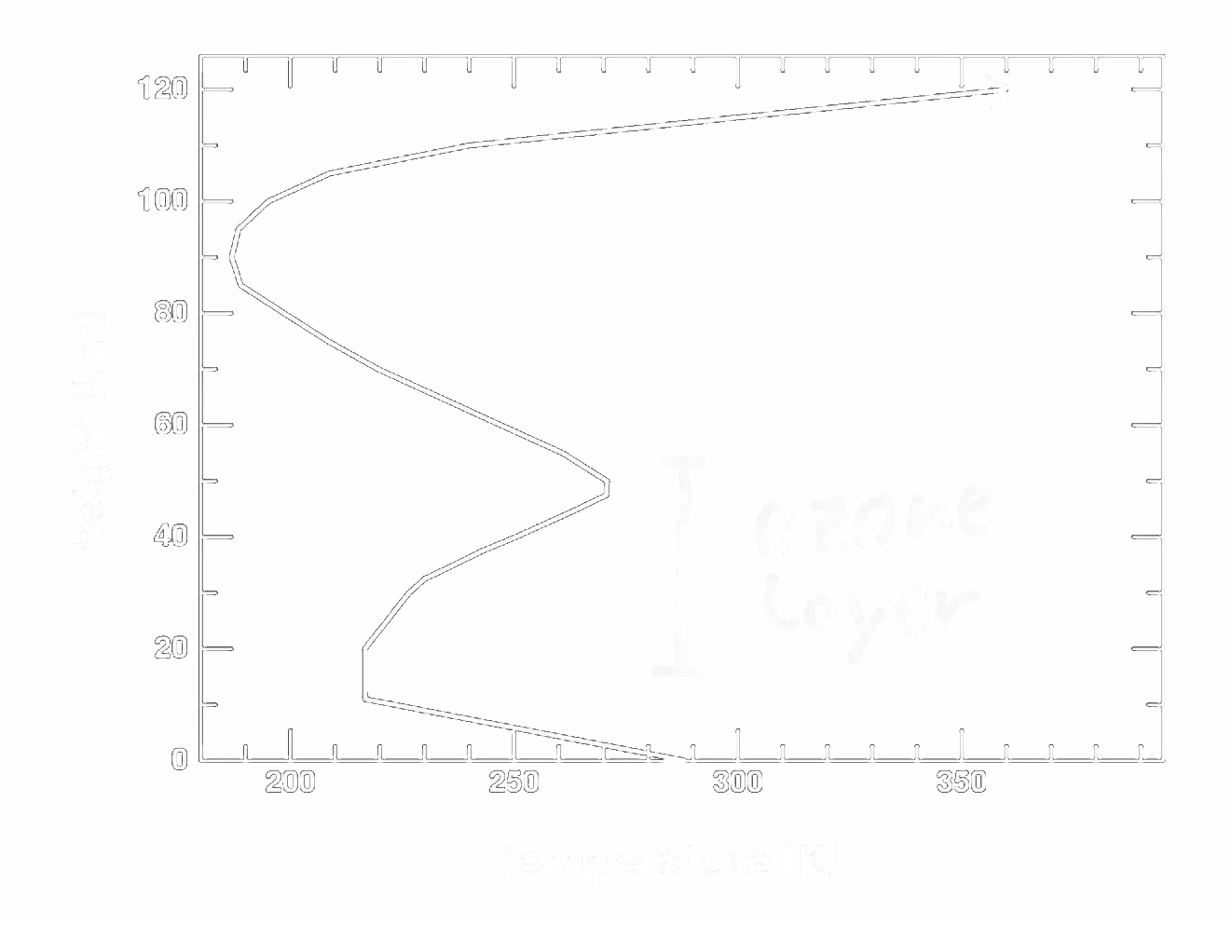
Of course now we could try to reproduce this temperature profile by extending the model with yet another type of radiation that gets absorbed in some middle layer, but I don't think there is really a point in doing that. I hope the model has already made it reasonably clear how the absorbed and emitted radiation of various layers can lead to such a temperature profile in a stationary atmosphere.

The stationary atmosphere is a good assumption for all but one layer of the atmosphere. Unfortunately, it is exactly the one layer that is most relevant for mountain temperatures: the troposphere. The troposphere is the lowest layer of the atmosphere (from the ground up to ~16 km), and we all know from our personal experience that with its wind and weather, it is anything but stationary.

In the last section, we will figure out why all the atmosphere is stationary, but the lowest layer is not, and we will see how this influences the temperature on top of a mountain.

Level 3 - Atmosphere in motion

The word troposphere is derived from the Greek word tropos (rotating) indicating that it is characterized by rotational convection mixing the air. Of course convection has a large influence on the temperatures of everything in that layer, also on the temperatures in the mountains. But when does convection occur?

From your school education you might remember that warm air is rising and cold air is sinking, which could explain convection. But actually, this is only half of the story. For air to rise it is not enough for it to be merely warmer than the air above. We need some more knowledge from meteorology, specifically about atmospheric stability, to fully understand mountain temperatures.

Atmospheric Stability

Atmospheric stability mainly depends on the rate at which the temperature decreases with altitude. This rate is called the lapse rate. The second important quantity is the rate at which the temperature of some air parcel changes as it rises or sinks due to work it does. (This will make more sense in a moment.)

The square in the following simulation represents a parcel of air, and you can drag it around to see how it behaves. The simulation assumes that no heat is transferred between the parcel and the surrounding air (adiabatic conditions). This is a reasonable assumption if the movement is fast compared to heat exchange processes, e.g., through radiation. Like before, the color indicates temperature.

If you move the parcel to higher altitudes, it expands and cools down (blueish color). The reason for the change in temperature is that while expanding, it has to use some of its energy to push away the surrounding air. If you move the parcel to lower altitudes, on the other hand, it is compressed. It gains energy and becomes warmer.

The rate at which the temperature of the parcel changes with altitude (when no heat is transferred) is the adiabatic lapse rate. In dry air, the adiabatic lapse rate is 9.8 °C/km.

Another important observation is that if you let go of the parcel, you can see that it floats back to its original height. In the simulation above, the surrounding atmosphere has a constant temperature. If you move the parcel up, it becomes colder than the surrounding. Colder air is denser. Therefore, it tends to sink back down. If you move the parcel down, it becomes warmer than the surrounding. Warmer air is less dense. Therefore, it tends to rise back up.

An atmosphere where the temperature is constant with altitude is very stable. Any parcel of air that is moved up or down for some reason moves back to its original height.

Let's see how this plays out for some other atmospheric temperature profiles. The following simulation covers three cases:

In the left case, the temperature of the atmosphere declines with altitude, but slower compared to the adiabatic lapse rate. A parcel of air that is moved up or down returns back to its original altitude, just like in the constant temperature case. The parcel of air starts out with a higher temperature compared to the air above but it still doesn't rise, because it would cool down too fast.

In the middle case, the temperature of the atmosphere declines exactly with the adiabatic lapse rate. Consequently, no matter where you move the parcel, it always turns out to have exactly the same temperature as its surrounding. Along with the same temperature comes the same density as its surrounding. The parcel is neutrally buoyant at any altitude.

In the right case, the temperature of the atmosphere declines faster than the adiabatic lapse rate. If you move the parcel up, its temperature goes down due to the work it has to do while expanding (just like in the other cases). However, this time the temperature of the parcel is not dropping as fast as the temperature of the surrounding air. Even though it is cooling down, it still turns out warmer than the surroundings. Warmer means less dense, and less dense means: it continues to rise. Accordingly, if you move the parcel down, it becomes warmer but not as warm as the surroundings. It turns out colder and denser than its surrounding and will continue to fall.

The adiabatic lapse rate is the edge case for atmospheric stability. If the temperature declines faster than the adiabatic lapse rate, the atmosphere becomes very unstable. Any parcel of air that is tipped out of balance will continue to rise or fall. Strong convection tends to emerge. This is, for example, what causes thunderstorms on a hot summer day, when the sun heats up the ground so much that the temperature differences go beyond the adiabatic lapse rate.

How does the adiabatic lapse rate influence mountain temperatures?

With the adiabatic lapse rate being the edge case for atmospheric stability, it creates a limit for how much temperature can decrease with altitude. Whenever the temperature declines faster than the adiabatic lapse rate, convection emerges which mixes up the atmosphere and works against the temperature differences.

In a lot of popular science sources, however, wind in combination with the adiabatic lapse rate is presented as the reason for low temperatures in the mountains. They claim that the air cooling down due to the work it does while rising to the top of a mountain leads to the low temperatures up there.

So which is it? Is wind in combination with the adiabatic lapse rate the reason for the low temperatures in the mountains, or would it be even colder without air movement?

In their book "Atmospheres", Goody and Walker have modeled an atmosphere without convection.

As we can see, without convection mixing up the atmosphere, it would be much warmer near the ground, and temperatures would decline with altitude much more rapidly.

This makes a lot of sense if you think about it. Convection is one of the pathways how heat is transported away from our planet's surface. Without this pathway, heat transfer would be less efficient, leading to higher temperature differences.

It is no coincidence that we use foamed materials (which are essentially immobilized air) for insulation. They are good at preserving high temperature differences because no convection can occur.

So, is it wrong to claim that it is colder in higher altitudes because of convection and the work done by the rising air? Well, yes and no. The temperature profile in the troposphere is sloped like it is because of convection and the adiabatic lapse rate. But it is also a fact that without convection, the temperature would decline even faster with altitude.

It is a bit like asking: "Why is the car moving with 80 km/h?" You could say it's because the motor is pushing the car forward, or you could say it is because the speed limit is 80.

The adiabatic lapse rate is the speed limit. It dictates the maximum, how fast temperatures can decline with altitude. The radiation absorbed near the ground and ultimately emitted back into space is the motor that actually drives the temperature differences.

Summary and Conclusion

Solar radiation of different wavelengths is absorbed in different layers of the atmosphere. With the highest intensity being in the visible range, and the atmosphere being transparent for visible light, most radiation is absorbed at the ground. Consequently, the atmosphere is mainly heated from below.

In the lowest layer of the atmosphere, the troposphere, this leads to such a strong temperature decline with altitude, that the atmosphere becomes unstable. The resulting convection counteracts the temperature differences. Thus, atmospheric stability limits the rate at which temperature can decrease with altitude.

The fact that air cools down due to the work it does as it rises (adiabatic lapse rate) is often presented as the reason for cold mountains. However, due to its implications on atmospheric stability, it also acts as a limit to temperature differences. If the temperatures in the mountains became lower and lower, at some point things would become unstable. The cold dense air would sink down, and warmer air would rise up.

Ultimately, the atmospheric temperature profile, and consequently the low temperature in the mountains, is the result of a complex interplay of various mechanisms. We haven't even touched many aspects like ground properties or humidity and cloud formation, If you wanted to pick only one reason for cold mountains, I think the radiative heat transfer discussed in level 1 is the best choice.